
Binary Search Explained — Popular SWE/SDET Interview Question
Binary Search Explained — Popular SWE/SDET Interview Question
Unlocking the Power of Binary Search: A Key Algorithm in Computer Science


Introduction
In the world of computer science, searching for data efficiently is crucial. Among the myriad of algorithms available, binary search stands out for its elegance and efficiency, especially when dealing with ordered data. This article dives into the fundamentals of binary search, contrasting it with linear search, and exploring its complexity through computational thinking and strong induction.
Basics of Searching Algorithms
Before diving into binary search, let’s briefly revisit linear search, a simple yet fundamental algorithm. Linear search involves examining each element in a list sequentially to find a target value. This method, while straightforward, has a linear time complexity of 𝒪(𝓃), meaning that in the worst case, every element in the list must be checked.
Limitations of Linear Search
Consider a scenario where you need to determine if a specific time slot, say Monday at 11 AM, is available in a list of scheduled meetings. If the list is unordered, linear search requires checking each time slot until the target is found or all slots are exhausted. This process can be time-consuming, particularly for large datasets.

Enter Binary Search

Binary search, on the other hand, leverages the power of order. 𝘉𝘺 𝘥𝘪𝘷𝘪𝘥𝘪𝘯𝘨 𝘵𝘩𝘦 𝘴𝘦𝘢𝘳𝘤𝘩 𝘴𝘱𝘢𝘤𝘦 𝘪𝘯 𝘩𝘢𝘭𝘧 𝘸𝘪𝘵𝘩 𝘦𝘢𝘤𝘩 𝘤𝘰𝘮𝘱𝘢𝘳𝘪𝘴𝘰𝘯, 𝘣𝘪𝘯𝘢𝘳𝘺 𝘴𝘦𝘢𝘳𝘤𝘩 𝘥𝘳𝘢𝘴𝘵𝘪𝘤𝘢𝘭𝘭𝘺 𝘳𝘦𝘥𝘶𝘤𝘦𝘴 𝘵𝘩𝘦 𝘯𝘶𝘮𝘣𝘦𝘳 𝘰𝘧 𝘤𝘰𝘮𝘱𝘢𝘳𝘪𝘴𝘰𝘯𝘴 𝘯𝘦𝘦𝘥𝘦𝘥. Let’s explore how this works.
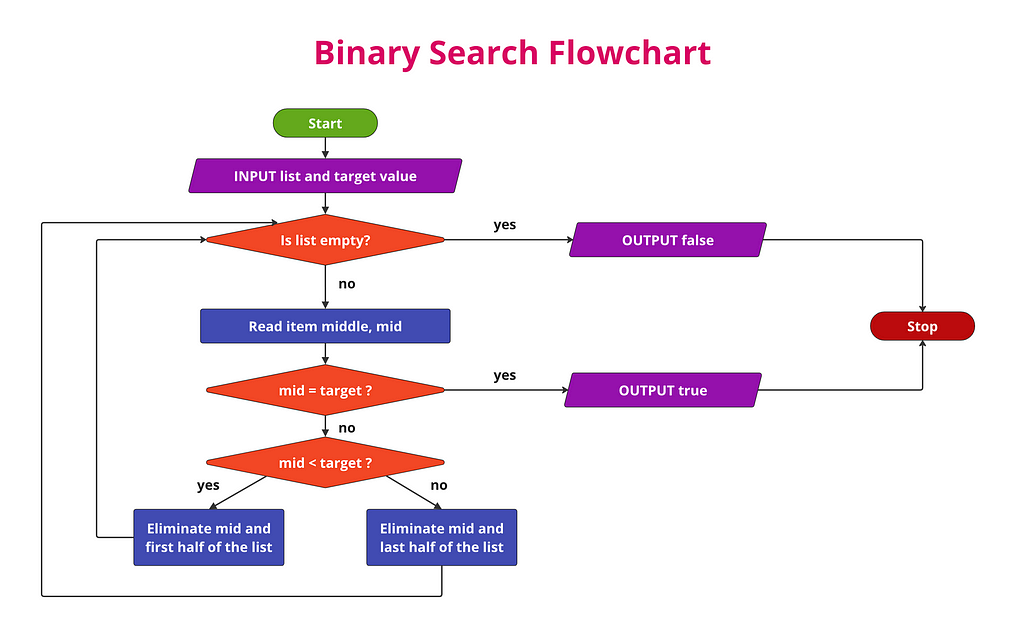
How Binary Search Algorithm Works
Problem: Determine whether a sorted list of values contains a target value.
Solution: Repeat these steps as long as the list of elements to consider is not empty:
- Compare the value in the middle of the list to the target.
- If they are equal, the we’ve found the target and can stop looking.
- If the value in the middle of the list is greater than the target, remove the middle element and elements that are larger than it, and repeat.
- If the value in the middle of the list is less than the target, remove the middle element and elements that are smaller than it, and repeat.
Continue this process, halving the list each time, until the target is found or the list is exhausted.
If we remove all elements in the list, then it doesn’t contain the target.
Example of Binary Search
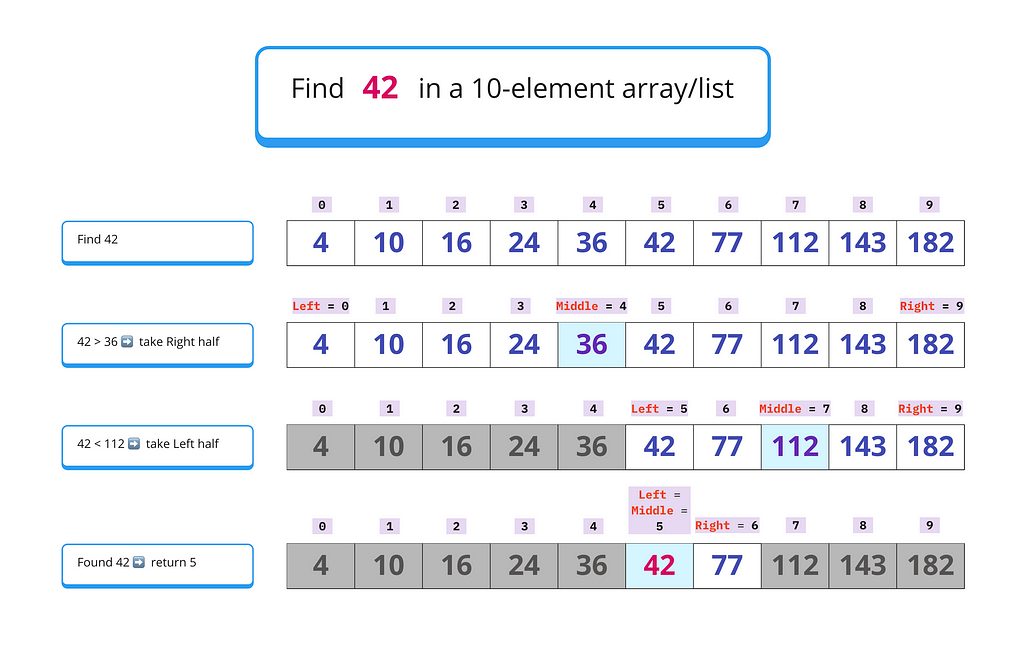
Imagine searching for the number 42 in the following sorted list:
[4, 10, 16, 24, 36, 42, 77, 112, 143, 182]
- If 42 were the middle element, it would have been an instant success!
- If 42 were not the middle element, the algorithm would determine whether to search the left or right half based on the comparison, effectively halving the search space each time.
Computational Complexity
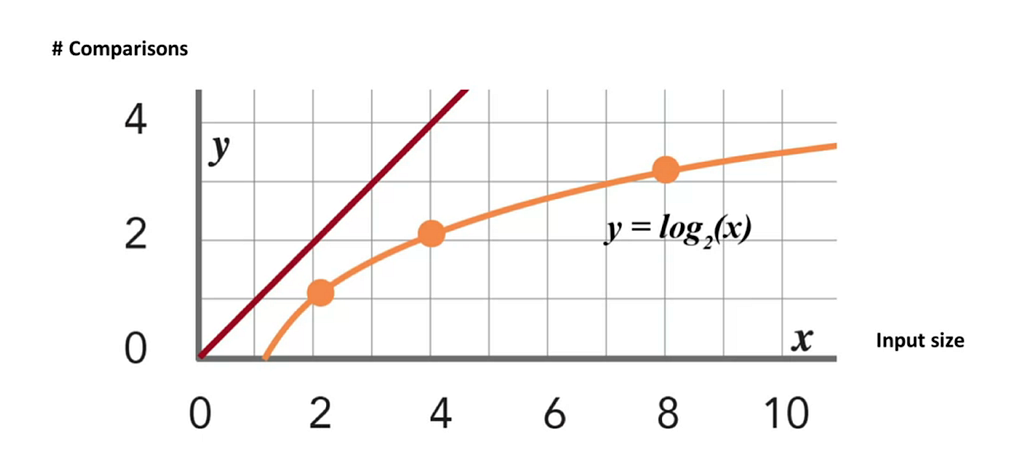
The beauty of binary search lies in its logarithmic complexity. While linear search has a worst-case complexity of 𝒪(𝓃), binary search operates in 𝒪(log 𝓃) time. This significant improvement means that even as the dataset grows exponentially, the number of comparisons grows logarithmically.

Visualizing the Complexity
To illustrate, if a list contains 1,000,000 elements, linear search might require up to 1,000,000 comparisons in the worst case. In contrast, binary search would need at most 20 comparisons: 𝒍𝒐𝒈₂(1,000,000) ≈ 20.

This efficiency is particularly advantageous for large datasets, where the difference in performance can be dramatic.
Ensuring Correctness with Strong Induction
Given its recursive nature, proving the correctness of binary search can be challenging. This is where strong induction becomes invaluable. Strong induction allows us to assume that a proposition holds for all values up to k and use this to prove it for k+1.
Inductive Proof of Binary Search
- Base Case: For n=0, where the list has only one element, binary search trivially works as it checks this single element.
- Inductive Step: Assume binary search works for all lists of length up to k. For a list of length k+1:
- Compare the target with the middle element.
- Depending on the result, binary search is recursively called on a sublist of length at most k, which, by the inductive hypothesis, works correctly.
By applying strong induction, we can rigorously prove that binary search correctly finds the target in a sorted list or determines its absence.

Practical Applications and Considerations
Binary search is widely used in computer science, from basic data retrieval operations to complex algorithms in databases and software engineering. However, it requires the data to be sorted beforehand, which can add an 𝒪(𝓃*log 𝓃) preprocessing step if the data isn’t already ordered.
In a technical coding interview, there is a high probability of being asked a binary search question. It’s an algorithm whose implementation you should know by heart, even when woken up in the middle of a night. So, I’ve provided 3 common LeetCode problems and solutions in Python below.

1️⃣ 𝑳𝒆𝒆𝒕𝑪𝒐𝒅𝒆 𝑬𝒙𝒆𝒓𝒄𝒊𝒔𝒆 # 1
704. Binary Search
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
Constraints:
- 1 <= nums.length <= 104
- -104 < nums[i], target < 104
- All the integers in nums are unique.
- nums is sorted in ascending order.
Solution
class Solution:
def search(self, nums: List[int], target: int) -> int:
# We consider the entire length of the array.
# Instantiate left pointer at 0, right at the last index of the array.
l, r = 0, len(nums) - 1
# Continue going until there are no more possibilities left or if we find the result.
# We do that by saying 'while our left pointer is <= to the right pointer'.
# When the pointers have crossed, we know there are no more values left to search.
# If they are both equal, it means we haven't looked at this value yet.
while l <= r:
# With each iteration of the loop, we're going to find the midway, which we get by:
# m = (l + r) // 2 - this may be a bug in a language other than Python.
# Python integers are unbounded, they can be infinitely large.
# But in other languages, like Java or C++, we may encounter an overflow.
# If we have a very large input array, and the l and r integers are very close to the 32-bit int max of ~2^31, then adding them together would possibly overflow, and we'd get the wrong result in the m value.
# To address that, calculate the mid point between left and right w/o adding them together.
# Take the distance between them with (r-l)//2. This gives us half of the distance between them.
# Then take that and add it the left index. Right is always >= left, we aren't adding but subtracting them. This will always be positive or zero.
m = l + (r - l) // 2
# If the value that the index is at is greater than the target, then we want to look at all values to the left of it.
if nums[m] > target:
# Set the right pointer to m - 1. We want to look at all values to the left. We're shrinking our criteria.
r = m - 1
# If that num is smaller than our target, then do the opposite. Set left to m + 1.
elif nums[m] < target:
l = m + 1
# If neither is true, we found our target. If it's not greater or smaller, it must be equal. We can return m as the result.
else:
return m
# If we went through every iteration of the loop and didn't find the result, then outside of it we should return -1 to indicate that.
return -1

2️⃣ 𝑳𝒆𝒆𝒕𝑪𝒐𝒅𝒆 𝑬𝒙𝒆𝒓𝒄𝒊𝒔𝒆 # 2
153. Find Minimum in Rotated Sorted Array
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
- [4,5,6,7,0,1,2] if it was rotated 4 times.
- [0,1,2,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.
Example 2:
Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.
Example 3:
Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times.
Constraints:
- n == nums.length
- 1 <= n <= 5000
- -5000 <= nums[i] <= 5000
- All the integers of nums are unique.
- nums is sorted and rotated between 1 and n times.
Solution
class Solution:
def findMin(self, nums: List[int]) -> int:
# We're going to maintain the result. We can set it to an arbitrary default value, such as nums[0] (the leftmost) or any other value in the nums array.
res = nums[0]
# Initialize left and right pointers.
l, r = 0, len(nums) - 1
# Keep running binary search, while our pointers are in a valid position.
while l <= r:
# If we ever get to the subarray that is already sorted,
if nums[l] < nums[r]:
# then we can update our result potentially, by setting the result to the minimum of itself and the leftmost value of this sorted portion.
res = min(res, nums[l])
# Break out of the while loop.
break
# If the array is not sorted, that's when we actually do our binary search portion, so that we can compute the mid pointer.
m = (l + r) // 2
# With this mid value, we're going to potentially update our result, setting the result to the minimum of itself and the value at the mid pointer.
res = min(res, nums[m])
# Now we need to know if we search to the left or to the right.
# How to determine that? We want to know if this mid value is part of the left sorted portion.
# It is a part of the left sorted portion, if the value at the mid index is greater than or equal to the value all the way to the left.
if nums[m] >= nums[l]:
# If it's a part of the left sorted portion, we want to search the right sorted portion. So we set our left pointer to mid+1.
l = m + 1
# The else case is if we're in the right sorted portion, in which case we want to search the left sorted portion. So we set our right pointer to mid-1.
else:
r = m - 1
# Keep doing that until we find the solution, or until the binary search has searched through the entire array.
# Return the result value.
return res
# Time: O(logn) - same as Binary Search
# Space: O(1)

3️⃣ 𝑳𝒆𝒆𝒕𝑪𝒐𝒅𝒆 𝑬𝒙𝒆𝒓𝒄𝒊𝒔𝒆 # 3
33. Search in Rotated Sorted Array
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Example 3:
Input: nums = [1], target = 0
Output: -1
Constraints:
- 1 <= nums.length <= 5000
- -104 <= nums[i] <= 104
- All values of nums are unique.
- nums is an ascending array that is possibly rotated.
- -104 <= target <= 104
Solution
class Solution:
def search(self, nums: List[int], target: int) -> int:
# Initialize pointers.
l, r = 0, len(nums) - 1
# Our condition is left <= right, because we may have an array with just one value [1]. Left and right are equal in that case, and we still have to check that one value.
while l <= r:
# Compute the mid value.
m = (l + r) // 2
# It's possible that mid value is the target. Then we simply return the index.
if target == nums[m]:
return m
# If that's not the case, we need to check which portion of the array are we in - left sorted or right sorted?
# Left Sorted Portion
# If mid value >= the left value (It's possible the mid value and the left value are the same.)
if nums[l] <= nums[m]:
# If the target is greater than the middle or less than the leftmost value in nums,
if target > nums[m] or target < nums[l]:
# Search the rightmost portion, update the left pointer.
l = m + 1
else:
# If the target is less than the middle and greater than the left,
# Search the left portion, update the right pointer.
r = m - 1
# Right Sorted Portion
else:
# If target is less than the middle and greater than the rightmost value,
if target < nums[m] or target > nums[r]:
# Search the left portion, update the right pointer.
r = m - 1
else:
# If target is greater than the middle and less than the right value, search the right portion of the array, update the left pointer.
l = m + 1
# If we find the result, we do a 'return m'.
# If we don't find it, we exit the loop and return -1.
return -1
Conclusion

Binary search is a powerful and efficient algorithm essential for any computer scientist’s toolkit. Its logarithmic complexity makes it vastly superior to linear search for large datasets, and its correctness can be ensured through strong inductive proof. By leveraging the ordered nature of data, binary search exemplifies the elegance and efficiency of algorithmic problem-solving in computer science.

𝓗𝒶𝓅𝓅𝓎 𝒸𝓸𝒹𝒾𝓃𝓰 𝒶𝓃𝒹 𝒹𝓮𝒷𝓊𝓰𝓰𝒾𝓃𝓰!
I welcome any comments and contributions to the subject. Connect with me on LinkedIn, X , GitHub, or Insta. Check out my website.
If you find this post useful, consider buying me a coffee.
Binary Search Explained — Popular SWE/SDET Interview Question was originally published in Women in Technology on Medium, where people are continuing the conversation by highlighting and responding to this story.
